Coherent illumination

Techniques like coherent diffraction, speckle spectroscopy, and ptychography require a coherent illumination of the sample. However, the wavefronts emitted by current (third generation) storage rings are still far from showing full lateral coherence. Stated differently, the photon beam emittance, that is, the product of the linear source size (rms) and the beam divergence (rms), is still several orders of magnitude above the diffraction limit, which is roughly 8 pm rad for 10 keV radiation. Hence, for the applications mentioned above only a coherent portion of the beam can be used while the rest has to be peeled off. In other words, one has to increase the lateral coherence length at the sample position by reducing the angular size of the (secondary) x-ray source, that is, the ratio of the lateral extent and the distance of the source. Furthermore, it is important to employ high quality optical components that minimize wavefront distortion.

Let us consider an example involving an undulator source at 12.4 keV with a width d_h = 120 μm and a height d_v = 20 μm (FWHM). A CRL consisting of 11 beryllium 2D lenses with R = 0.05 mm at a distance L₁ = 80 m from the source yields a secondary source at a distance L₂ = 1045 mm (Figure 1). A sample is illuminated coherently by the full wave front of the secondary source provided that the effective aperture D_eff = 393 µm of the CRL is not larger than the lateral coherence length of the wavefront at L₁ = 80 m. The lateral coherence length is λ L₁ / d_h = 67 µm horizontally and λ L₁ / d_v = 400 µm vertically. Hence, while the secondary source is diffraction limited in the vertical direction this is not the case in the horizontal direction, despite the large source-to-sample distance.

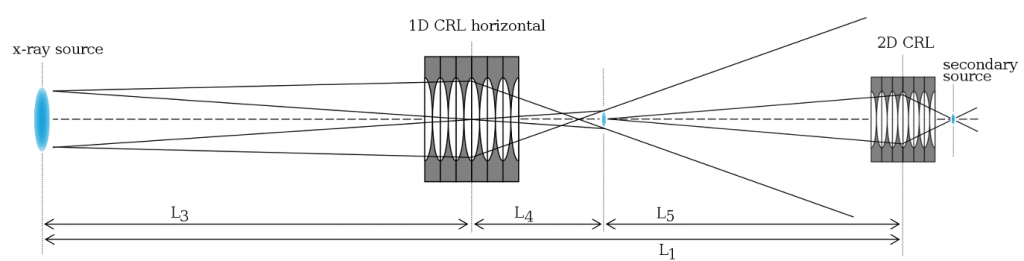
A remedy for the horizontal direction can be obtained by placing beryllium 1D lenses half way between the source and the 2D CRL in order to reduce the angular source size in the horizontal direction (Figure 2). A CRL consisting of 24 1D lenses with R = 0.3 mm at a distance L₃ = 40 m from the source yields a secondary source at a distance L₄ = 3043 mm. The horizontal extent (FWHM) of this source is s_h = 9 μm with a horizontal coherence length λ L₅ / s_h = 411 μm at the 2D CRL. The lateral extent (FWHM) of the secondary source is 0.33 µm horizontally and vertically. Hence, this way we obtain a circular, Gaussian, diffraction limited secondary source.

Note that it is impossible to achieve this with the aid of slits. For a circular, coherent secondary source one would have to place a slit with a width of roughly 20 μm right at the physical source (which is impossible) or a slit with a width of less than a micrometer (which doesn’t exist) at the secondary source. Furthermore, slits tend to destroy the Gaussian profile and introduce ringing.